Rozdział 3 Testy rozkładu

Aby zrozumieć ten rozdział należy zapoznać się z rozdziałem Podstawy.`

Jednym z podstawowych kryteriów stosowalności technik statystycznych jest rozkład danych, do którego konkretna technika zostanie użyta. W podstawowych zastosowaniach biostatystycznych interesuje nas właściwie jedynie czy rozkład populacji jest normalny(Gaussowski), czy nie. Rozkład populacji staramy się ustalić na podstawie zebranej próby, więc w tym celu stosujemy odpowiednie testy statystyczne. Najbardziej uniwersalnym i w obecnych czasach najbardziej rozpowszechnionym testem używanym do tego celu wydaje się test Shapiro-Wilka. Historycznie najczęściej używany był test Kołmogorowa-Smirnowa, jednak okazał się on nie dość czuły. Dla dużych grup oba testy z całą pewnością dadzą ten sam wynik.

Hipotezą zerową testu Shapiro-Wilka jest: “ten rozkład jest normalny”. W związku z tym, jeżeli nasz program komputerowy poda wynik p<0,05, to odrzucamy hipotezę o normalności rozkładu, czyli stwierdzamy “ten rozkład nie jest normalny”. Jeżeli otrzymujemy p>=0,05 (większe lub równe 0,05), to nie odrzucamy hipotezy o normalności rozkładu i od tej chwili traktujemy ten rozkład jak rozkład normalny. 

W tym miejscu możemy przedstawić krótką tabelkę podającą sposób radzenia sobie z dwoma rodzajami rozkładów:

typ rozkładu	test statystyczny	parametry rozkładu
normalny	parametryczny	średnia, odchylenie standardowe
inny niż normalny	nieparametryczny	mediana, IQR

Przyjrzyjmy się prostemu przykładowi. Przeanalizujemy zbiór zawierający wzrost i masę ciała piętnastu Amerykanek. Zbiór można pobrać w formacie Excela tutaj, a w formacie pliku tekstowego csv tutaj. Dane te są częścią darmowego pakietu statystycznego R.

Ładujemy dane do naszego wybranego programu statystycznego i wybieramy test Shapiro-Wilka. Dla zmiennej “height” p>0.05 (p=0.754), więc traktujemy rozkład jako rozkład normalny. Dla zmiennej “weight” również p>0.05 (p=0.699), więc jak poprzednio, w dalszych rozważaniach przyjmujemy, że jest to rozkład normalny. Zwróćmy uwagę, że nie padło kategoryczne “jest to rozkład normalny”, ponieważ ściśle rzecz biorąc po prostu nie znaleźliśmy dowodów, że ten rozkład nie jest normalny. Jest to jednak tylko niuans, który nic nie zmienna w sposobie w jaki dalej będziemy traktowali dane.

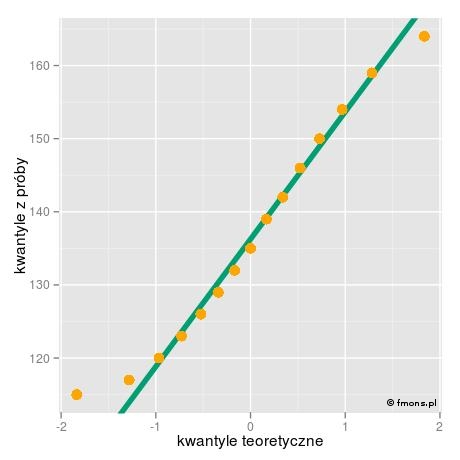
Istnieją również wizualne metody sprawdzenia, czy dane mogą pochodzić z rozkładu normalnego. Jedną z najczęściej używanych technik jest wykres QQ (qqplot), czyli wykres kwantyl kwantyl.  Technika ta jest bardzo ściśle związana z testem Shapiro-Wilka. Przykład takiego wykresu dla zmiennej “wieght” z analizowanego tutaj zbioru zamieszczony jest obok. Interpretacja jest następująca: jeżeli punkty wykresu leżą blisko prostej i są równomiernie rozłożone po jej jednej i drugiej stronie (np. naprzemiennie), to dane pochodzą z rozkładu normalnego. Na naszym rysunku widać drobne odstępstwa w przypadku punktów na samej górze i na samym dole - punkty te leżą dalej od prostej niż pozostałe punkty. Jednak odstępstwo to jest na tyle małe, że test Shapiro-Wilka nie stwierdza odstępstw od rozkładu normalnego (patrz test przeprowadzony wyżej i wartość p w nim uzyskana). 

Wizualny test przy pomocy wykresu QQ jest często podstawą do przyjęcia normalności jakiegoś zbioru, mimo że formalne testy mówią, że rozkład normalny nie jest. Stać się tak może na przykład gdy dane są mocno zdyskretyzowane (np. zaokrąglone), nie będziemy się jednak wgłębiać w ten przypadek i poprzestaniemy na samy stwierdzeniu, że może się  tak zdarzyć. 

3.1 Program statystyczny: wykres kwantyl-kwantyl (qq-plot) i test Shapiro Wilka

Poniżej zamieszczony program służy rysowaniu wykresu kwantyl-kwantyl z dostępnych danych (np. z danych zawartych w jednej kolumnie w arkuszu kalkulacyjnym) oraz do przeprowadzenia testu normalności Shapiro-Wilka. Aby z niego skorzystać wpisujemy dane do pierwszego pola, oddzielając liczby spacjami (można używać zarówno kropki jak i przecinka dziesiętnego: można wpisać zarówno 1,1 jak i 1.1) lub wklejamy dane z Excela bądź LibreOffice (OpenOffice) - ten diagram demonstruje jak to zrobić. W następne pole wpisujemy tytuł wykresu (który pojawi się na górze). W kolejnych dwóch polach podajemy opis osi (np. moglibyśmy chcieć opisać osie po angielsku: “theoretical quantiles” na osi x i “sample quantiles” na osi y. Potem wybieramy tylko kolor punktów na wykresie i gotowe. Pod wykresem znaleźć można wynik testu Shapiro-Wilka, dotyczącego normalności wprowadzonych danych.