Rozdział 4 Porównania dwóch grup

Aby zrozumieć ten rozdział należy zapoznać się z rozdziałem Podstawy.  Warto również zapoznać się z rozdziałem Testy rozkładu

Jednym z najczęstszych zadań statystycznych jest stwierdzenie, czy dwie grupy się różnią. Możemy na przykład zapytać, czy ciśnienie tętnicze w grupie 100 osób z chorobą wieńcową jest wyższe niż u 100 osób zdrowych (nie jest to zbyt ambitne zadanie), lub czy dzieci z rodzin o dochodzie poniżej 1000 zł na osobę mają lepszą średnią ocen niż dzieci z rodzin o wyższym dochodzie.

4.1 Test t

Na początku musimy odpowiedzieć sobie na pytanie, co porównujemy i w jaki sposób. Okazuje się, że najczęściej używanym testem jest test t, który porównuje średnie porównuje się średnie w obu grupach. Szczegóły matematyczne tego testu nie są dla nas interesujące, poza dwiema informacjami: po pierwsze test t wymaga, aby rozkład danych był normalny, po drugie test ten bierze pod uwagę odchylenia standardowe w obu grupach. Pierwsza informacja wpływa na sposób w jaki analizujemy dane - druga niekoniecznie.

Jeżeli chcemy więc porównać dwie grupy, zaczynamy od sprawdzenia rozkładu w obu grupach. Może się tak zdarzyć, że już przed przystąpieniem do porównywania wiemy, że jakaś zmienna ma (lub nie) rozkład normalny. Wtedy po prostu stosujemy (lub nie) test t. Jeżeli nie mamy tej wiedzy, to sprawdzamy rozkład danych, na przykład przy pomocy technik opisanych w rozdziale Testy Rozkładu.

Przeanalizujmy dane pochodzące z badań nad anoreksją u młodych kobiet. W badaniu porównywano efekty kognitywnej terapii behawioralnej (CBT - Cognitive Behavioral Treatment) i terapii rodzin (FT - Family Treatment) w leczeniu tej choroby. Jedną z grup badawczych, oprócz CBT i FT, była grupa kontrolna, w której nie prowadzono żadnej terapii. Masy pacjentek zmierzono po raz pierwszy przed rozpoczęciem terapii a po raz drugi po ich zakończeniu.

Na początek porównajmy masy grupy kontrolnej i grupy CBT przed przystąpieniem do badania. Dane dla grupy kontrolnej można pobrać tutaj(w formacie Excela) lub tutaj (w formacie csv) a dla grupy CBT tutaj (Excel) lub tutaj (csv).

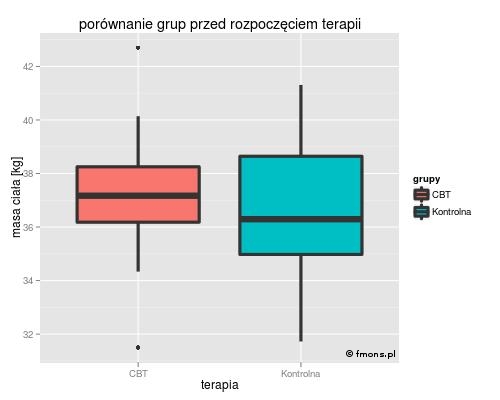
Graficznie dane można zaprezentować na przykład tak jak na rysunku obok przy użyciu wykresów typu boxplot (po polsku - pudełko-z-wąsami (serio!!!)). Ta technika graficzna jest intuicyjnie zrozumiała, a jej szczegóły opisane są w dodatku I - Podstawowe Techniki Graficzne (niegotowe… przyp. autora).

Załadowanie danych do programu przeglądarkowego t.test umieszczonego na dole strony (lub do innego programu statystycznego) daje w wyniku wartość p=0,4343. W teście hipotezą zerową jest “te dane nie różnią się od siebie”, a wartość p>0,05 oznacza, że nie mamy wystarczających powodów, aby ją odrzucić. Będziemy więc traktowali obie grupy jako takie same.

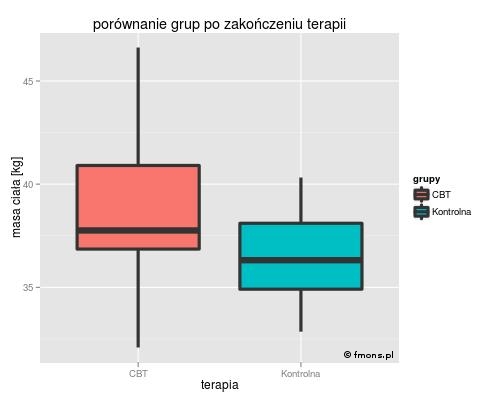
Sprawdziliśmy, że grupa w której przeprowadzono terapię CBT i grupa kontrolna nie różnią się na początku badania. Sprawdźmy więc, czy różnią się po jego zakończeniu. Rysunek przedstawiono obok, po lewej stronie. Z samego rysunku widać, że masa dziewcząt poddanych terapii wyraźnie wzrosła, a test t tylko to potwierdza, dając w rezultacie wartość p=0,0147. Otrzymany wynik p<0,05 sprawia, że odrzucamy hipotezę zerową i uznajemy, że grupy się różnią - z wykresu widzimy, że grupa CBT przyjmuje wyższe wartości.

4.2 Sparowany test t

Najciekawszym pytaniem w analizowanych danych jest jednak nie to, czy grupy kontrolna i leczona CBT różnią się na końcu badania, tylko czy osoby z grupy leczonej przy pomocy CBT przybrały na wadze. Moglibyśmy zrobić to samo co poprzednio, czyli wrzucić dane z grupy CBT przed terapią i po terapii do programu obliczającego test t w dokładnie taki sam sposób jak w poprzednim paragrafie. Postępując w ten sposób zignorowalibyśmy jednak bardzo ważną informację, a mianowicie, że zarówno przed jak i po terapii mamy do czynienia z tymi samymi osobami. Ignorowanie dostępnych informacji jest jednym z podstawowych grzechów statystycznych. Grzeszyć nie chcemy, więc użyjemy wersji testu t, która „wie”, że dane są sparowane. Testu tego możemy użyć, gdy w obu grupach mamy te same osoby, lub gdy przypadki w obu grupach zostały celowo dobrane w pary, na przykład ze względu na wiek, przebieg choroby czy dane antropometryczne.

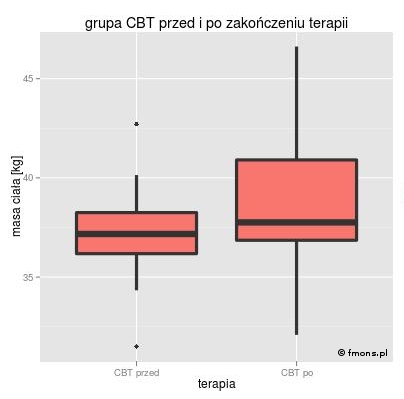
W naszym przypadku rysunek pokazuje, że po zastosowaniu terapii masa ciała wzrasta.Jeżeli zastosujemy niesparowany test t, t wartość p=0,1005, czyli zgodnie z przyjętą zasadą powinniśmy przyjąć, że terapia nie dała żadnego efektu. Jednak gdy wykorzystamy pełną dostępną informację, czyli użyjemy testu sparowanego, uzyskamy wartość p=0,0350. Test potwierdza to co widzimy gołym okiem na rysunku - terapia przyniosła efekty. Niesparowany test t „nie widzi” tego wyniku najprawdopodobniej z powodu dużej zmienności oraz małej liczebności grupy.

Powyższe obliczenia można powtórzyć przy pomocy programu zamieszczonego na dole tej strony zaznaczając i odznaczając pole „test sparowany”.

4.3 Gdy dane nie są normalne - test Wilcoxona

W przypadku każdego z powyższych testów powinniśmy zacząć od sprawdzenia normalności rozkładu danych, tak jak przedyskutowano i zademonstrowano to w rozdziale Testy rozkładu. Dla wszystkich danych analizowanych do tej pory otrzymujemy wynik, że dane możemy traktować jako pochodzące z rozkładu normalnego. Zainteresowany Czytelnik może sprawdzić to stwierdzenie zapoznając się z rozdziałem Testy rozkładu i stosując program tam zamieszczony do przetestowania danych z tego rozdziału. Co jednak zrobić, gdy okaże się, że dane nie mają rozkładu normalnego?

W takim przypadku powinniśmy zastosować nieparametryczny test Wilcoxona. Test ten porównuje mediany a nie średnie, ale dla zastosowania go w praktyce nie ma to znaczenia. Test Wilcoxona nie zakłada rozkładu normalnego (ani żadnego innego), dlatego można go zastosować, gdy dane nie mają Gaussa. Mamy tutaj jednak do czynienia z typowym przypadkiem „coś za coś”: test można zastosować w większej liczbie przypadków, jednak jest on zdecydowanie mniej czuły niż test t, więc częściej można „nie zauważyć” efektu. Test Wilcoxona również może być niesparowany i sparowany, co znajduje swoje odzwierciedlenie w programie na dole strony. Zachęcam Czytelnika do powtórzenia wszystkich obliczeń w tym rozdziale przy zastosowaniu testu Wilcoxona w miejsce testu t.

Dodajmy jeszcze, że jak już wspomnieliśmy, niewykorzystanie pełnej dostępnej informacji jest grzechem statystycznym. W związku z tym, w sytuacji gdy wiemy, że dane mają rozkład normalny, nie powinniśmy stosować testu Wilcoxona.

4.4 Testy dwustronne i jednostronne

W analizach z tego rozdziału zawsze interesowało nas, czy coś jest większe od czegoś innego - konkretnie, czy masa ciała po zastosowaniu terapii jest większa niż przed. Testy statystyczne, które przeprowadzaliśmy dawały nam odpowiedź na pytanie tylko czy dane grupy się różnią, a nie czy któraś z nich jest większa. Innymi słowy, jeżeli sprawdzamy, czy masa po terapii zwiększyła się, to test da nam pozytywną odpowiedź zarówno w przypadku gdy masa istotnie się zwiększyła jak i w przypadku gdy istotnie się zmniejszyła. Test taki nazywamy testem dwustronnym. W naszym przypadku, to które wyniki są większe odczytywaliśmy z rysunku. Można jednak przeprowadzić tak zwany test jednostronny, w którym od razu pytamy, czy wartości w wybranej grupie (np. po zakończeniu terapii) są większa, a nie czy jest po prostu różne. Ponieważ jest to jedyny przypadek w którym spotykamy się z testem jednostronnym w tym podręczniku, nie będziemy dale zgłębiać tematu. Zainteresowany Czytelnik może pogłębić swoją wiedzę przy pomocy bardziej zaawansowanych źródeł.

4.5 Ostatnia uwaga

Zdarzyło mi się, że przekonywano mnie z żarliwością lepszej sprawy, że w sytuacji, gdy porównywane grupy nie mają rozkładu normalnego, należy użyć testu Manna-Whitneya, a nie „jakiegoś Wilcoxona”. Otóż oba testy, mimo że używają innej terminologii, są sobie całkowicie równoważne i wartości p są zawsze takie same dla tych samych danych.

4.6 Program statystyczny: test t i test Wilcoxona

Poniżej zamieszczony program służy testowania równości dwóch średnich (dla testu t) i median (dla testu Wilcoxona). Dla porównywanych zbiorów rysowane są wykresy typu „pudełko-z-wąsami”. Aby z niego skorzystać wpisujemy dane w dwa pierwsze pola (pierwsza zmienna w pierwsze pole, druga w drugie), oddzielając liczby spacjami (można używać zarówno kropki jak i przecinka dziesiętnego: można wpisać zarówno 1,1 jak i 1.1) lub wklejamy dane z Excela bądź LibreOffice (OpenOffice) - ten diagram demonstruje jak to zrobić. W następne dwa pola wpisujemy nazwy zmiennych (np. „grupa badana” oraz „grupa kontrolna”), który pojawią się na osi x W kolejnym polu podajemy nazwę osi y (np. „masa ciała (kg)”). Potem wybieramy tylko kolor punktów na wykresie i gotowe. Pod wykresem znaleźć można wartości p dla wybranego testu. Dla purystów statystycznych dodamy, że poniższy program używa poprawki Welcha, więc wariancje nie muszą być równe.