Rozdział 2 Podstawy

W tym rozdziale zdefiniowane zostaną podstawowe pojęcia niezbędne do zrozumienia statystyki od strony praktycznej. Przed przeczytaniem któregokolwiek z późniejszych rozdziałów należy zapoznać się z materiałem zawartym w tym miejscu.

2.1 Populacja i próba

W analizie statystycznej zazwyczaj chodzi nam o opisanie pewnej cechy populacji, to znaczy wszystkich osób (przedmiotów, zjawisk), którymi jesteśmy zainteresowani. Na przykład w badaniach nad lekiem może interesować nas populacja wszystkich osób po zawale serca. Populacja nie musi być tak szeroka - może nas interesować na przykład populacja wszystkich mężczyzn powyżej 70 roku życia, palących, z nadciśnieniem tętniczym i wzrostem powyżej 175 cm. Innymi słowy, populacja to zbiór, który możemy opisać zaczynając zdanie od „wszystkie osoby, które:”.

Zazwyczaj nie mamy luksusu zbadania całej populacji, wybieramy więc z niej próbę, czyli pewną skończoną liczbę osób, które spełniają naszą definicję zaczynającą się jak powyżej od „osoby, które:”. Liczebność tej próby zazwyczaj wynika z środków dostępnych na jej zebranie, zawsze jednak należy dążyć do pozyskania największej możliwej liczby osób, spełniających naszą definicję. Dodatkowo, próba powinna być wybrana z populacji całkowicie losowo.

2.2 Estymacja

Mając do dyspozycji pewną próbę obliczamy dla niej różne wielkości, takie jak na przykład średnia czy odchylenie standardowe (patrz niżej). Jeżeli rozszerzamy ten wynik na całą populację, to znaczy, że estymujemy,lub inaczej szacujemy, daną wielkość, czyli na przykład wspomnianą średnią. Załóżmy dla ilustracji, że chcemy poznać wzrost mężczyzn pomiędzy 25 a 35 rokiem życia mieszkających w Zielonej Górze. Losujemyz tej grupy 100 mężczyzn, mierzymy ich wzrost i obliczamy średnią. Jeżeli przyjmiemy, że ta średnia jest średnią dla wszystkich mężczyzn w wieku pomiędzy 25 a 35 w interesującym nas mieście, to znaczy, że estymujemy średnią wzrostu populacji przy pomocy próby. Zwykle przy estymowaniu różnych parametrów podajemy również dokładność, z jaką przeprowadziliśmy estymację.

2.3 Rozkład pomiarów

Powróćmy do przykładu ze wzrostem - tym razem niech będzie to wzrost wszystkich kobiet w Polsce (w momencie pisania tych słów). Z doświadczenia wiemy, że bardzo niewiele jest kobiet o bardzo niskim wzroście (powiedzmy pomiędzy 130 cm a 140 cm), podobnie jak bardzo niewiele jest kobiet o wzroście bardzo wysokim (na przykład 180 cm do 190 cm). Im bliżej średniej jest wybrany przez nas przedział, tym więcej kobiet w nim znajdziemy. Na przykład na pewno zdecydowanie więcej jest kobiet pomiędzy 155 a 165 niż w którymkolwiek z powyżej podanych przedziałów.

Jeżeli naniesiemy liczbę pań w każdym przedziale na wykres, to otrzymamy histogram. W naszym przykładzie będzie wyglądał on następująco:

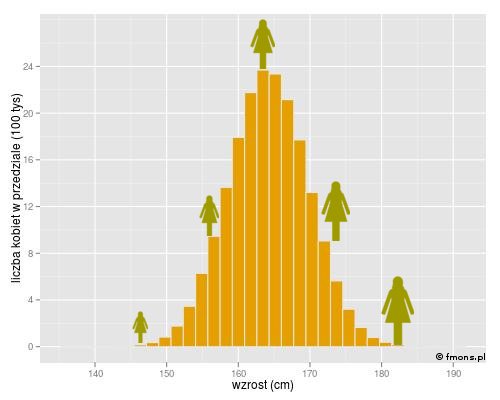
Szerokość słupków wynosi 2 cm, a ich wysokość odpowiada liczbie pań zawartych w tym dwucentymetrowym przedziale. Czyli na przykład w najwyższym słupku znajdują się panie o wzroście od 163 do 165 cm i jest ich ponad 2 miliony. Po lewej stronie słupki są bardzo niskie - oznacza to, że jest bardzo niewiele pań o niskim wzroście. Podobnie po prawej stronie: słupki są niskie, więc bardzo wysokich pań jest również niewiele.

Rozkład tego typu, to znaczy dane, w których średnia i wartości bliskie średniej są reprezentowana najczęściej, a wartości skrajne najrzadziej, jest spotykany w statystyce (i w ogóle w życiu) bardzo często. Nazywamy go rozkładem normalnym, a jego kształt często opisuje się określeniem krzywa dzwonowa(lub krzywa Gaussa). Istnieją inne rozkłady o podobnym kształcie, ale w tym podręczniku nie będziemy się nimi zajmować.

Inne zjawiska/pomiary, mają inne rozkłady - każdy rozkład ma swój kształt i odpowiada mu pewien wygląd histogramu.

W naszym przykładzie dotychczas nie robiliśmy różnicy pomiędzy populacją a próbą. Założyliśmy, że mogliśmy zmierzyć wszystkie kobiety w Polsce i narysować dla nich histogram, przez co nasze rozważania są trochę teoretyczne, nierzeczywiste (ściśle - zasymulowane). Prawie zawsze rysujemy histogram dla konkretnej próby, obliczamy średnią i odchylenie standardowe i za ich pomocą wnioskujemy jak wygląda rozkład populacji.

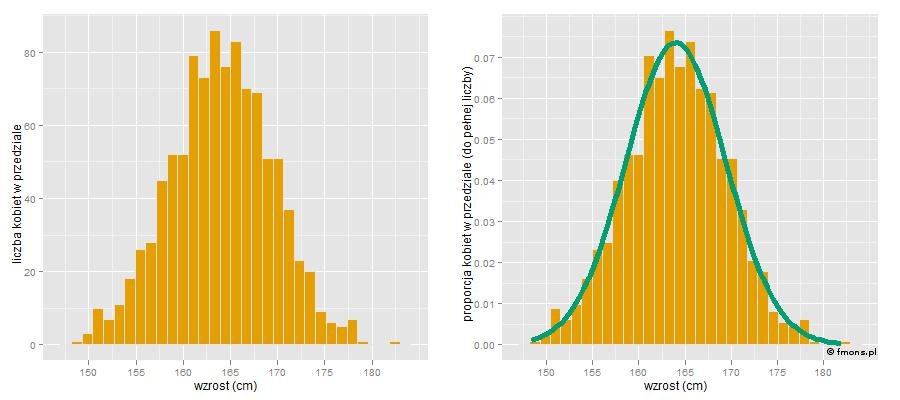
Pokażmy więc rozkład próby pewnej liczby pań wylosowanych z pełnej populacji. Na pierwszym z poniższych rysunków widzimy histogram wzrostu dla 1000 pań. Jak widać słupki są znacznie niższe (mniej pań w każdym przedziale wzrostu) a histogram jest bardziej poszarpany. Dla tej podgrupy histogram nie jest po prostu zmniejszoną wersją histogramu dla pełnej grupy! Różni się bardzo w szczegółach i nawet średnia i odchylenie standardowe są inne. Na drugim z poniższych rysunków na osi y, zamiast liczby pań w danym przedziale, umieściliśmy proporcję, czyli liczbę pań w danym przedziale podzieloną przez liczebność całej grupy (czyli 1000). Jeżeli “wygładzimy zęby” histogramu, to otrzymamy coś, co bardzo nieformalnie możemy nazwaćrozkładem prawdopodobieństwa (zielona linia). Tutaj wysokość pole (wysokość razy szerokość (czyli 2cm)) słupka odpowiada prawdopodobieństwu, że wylosowana przypadkowo kobieta znajdzie się w przedziale odpowiadającym temu słupkowi.

Posługując się rozkładem prawdopodobieństwa, komputer jest w stanie wyliczyć prawdopodobieństwo uzyskania danego zbioru wyników (oraz wyników bardziej skrajnych). Innymi słowy, jeżeli okaże się, że w grupie 10 kobiet, którą analizujemy jest 10 pań o wzroście pomiędzy 140 a 150 cm, komputer powie nam, jakie jest prawdopodobieństwo uzyskania takiego (i jeszcze bardziej skrajnego czyli zawierającego jeszcze niższe panie) wyniku. Z dotychczasowych rozważań możemy się domyślać, że to prawdopodobieństwo będzie bardzo małe. To, że powyżej napisałem w nawiasie “i jeszcze bardziej skrajnych” wynika z powszechnie przyjętej metodologii statystycznej - bez tego zastrzeżenia opis ten byłby błędny, jednak na użytek praktyka można specjalnie się nad nim nie zastanawiać.

TUTU ### Średnia i odchylenie standardowe

Dotychczas posłużyliśmy się kilka razy pojęciem średnia oraz odchylenie standardowe, zakładając, że są one albo znane Czytelnikowi, albo intuicyjnie zrozumiałe. W tym miejscu napiszemy kilka słów na temat tych wielkości.

Intuicyjne zrozumienie średniej jest zwykle prawidłowe. Średnia to jedna z kilku wielkości starająca się znaleźć „środek” zbioru danych (próby) lub populacji. Obliczamy ją dodając do siebie wszystkie wartości i dzieląc przez ich liczbę. Trzymając się przykładu ze wzrostem, jeżeli chcemy obliczyć średnią 100 pań, dodajemy ich wzrost i dzielimy przez 100.

Średnia to miara „środka”, jednak sam środek nie daje wystarczającej wiedzy o grupie. Jeżeli badamy grupę 100 bokserów wagi średniej, to średnia dla tej grupy wynosi około 71 kg, ale wszyscy mieszczą się w przedziale 70-72,5 kg. Jeżeli wyobrazimy sobie grupę 100 pasażerów samolotu, to średnia waga też może wynosić 71 kg, jednak rozrzut wag poszczególnych osób będzie znacznie większy - od małych dzieci, po wysokich i otyłych dorosłych. Mówiąc (bardzo) potocznie, przypadkowy pasażer z naszego samolotu będzie „średnio” dalej od średniej (dla pasażerów samologu) niż przypadkowy bokser (od średniej dla wszystkich bokserów w tej wadze). Tę odległość od średniej mierzy odchylenie standardowe.

Nie będziemy przytaczać żadnych wzorów, ponieważ i tak obliczenia statystyczne wykonuje komputer, a naszym celem w tym podręczniku nie jest kształcenie intuicji matematycznej, tylko próba nauczenia się praktycznego stosowania statystyki. Z tego samego powodu nie będziemy wprowadzali szczegółowo pojęcia średniej ważonej, która, dla danych najczęściej spotykanych w naukach biomedycznych, jest równoważna zwykłej średniej - to zagadnienie pozostawimy bardziej zaawansowanemu kursowi statystyki.

2.3.1 Inne miary tendencji centralnej: mediana i moda

Średnia jest miarą „środka”, czyli „centrum”. Choć miara ta jest najbardziej rozpowszechniona, nie jest ona jedyną. W biostatystyce oprócz średniej najczęściej używa się mediany. Ponownie używając potocznego języka, mediana jest to wartość dokładnie w środku zbioru, który został uszeregowany od wartości najmniejszej do wartości największej. Czyli na przykład medianą zbioru wag pięciu osób (50, 60, 88, 71, 82 kg) jest 71 kg, ponieważ po uporządkowaniu mamy (50, 60, 71, 82, 88 kg). Średnia dla tego zbioru to 70,2 kg. Po co w ogóle używać mediany? Wielkość ta jest wykorzystywana w przypadkach, w których rozkład danych (patrz wyżej) nie jest normalny (Gaussowski), czyli nie jest taki jak na rysunkach 1, 2, 3. Najczęściej używanym przykładem są wynagrodzenia.

Załóżmy, że w fabryce pracuje 100 robotników zarabiających 1500 zł i jeden dyrektor zarabiający 25000 zł. Średnia płaca w tej fabryce wynosi 1732,67 zł, co tak naprawdę nie jest w żaden sposób reprezentatywne: ani żaden robotnik, ani tym bardziej dyrektor, tyle nie zarabia! Dla poszukującego pracy robotnika lepszą informacją o tym ile zarobi jest mediana, wynosząca tutaj 1500 zł. Oczywiście rozkład płac w tej fabryce niczym nie przypomina rozkładu normalnego. W zastosowaniach biostatystycznych często mamy do czynienia z takimi „nieuczesanymi„ rozkładami.

Tym czym dla średniej jest odchylenie standardowe, tym dla mediany jest wielkość zwana IQR, czyli odstęp międzykwartylowy. Wielkość tę opiszemy w późniejszym rozdziale.

Inną, już nie tak często używaną miarą jest moda. Jest to po prostu wartość występująca najczęściej. Definicja ta komplikuje się dla danych ciągłych, które w zbiorze występują tylko raz, ale nie musimy się tym przejmować, ponieważ modę liczy komputer. Tak na marginesie, to istnieją sytuacje, w których definicja mediany też się komplikuje, ale podobnie jak poprzednio, jest to zmartwienie programistów statystycznych, a nie użytkownika statystyki.

2.3.2 SEM - czyli błąd standardowy średniej

Odchylenie standardowe i SEM to miary często mylone. SEM jest wielkością bardzo istotną dla interpretacji wielu testów statystycznych, więc warto poświęcić mu kilka słów. Jest to dość trudne zagadnienie, więc ten fragment może wymagać kilkukrotnego przeczytania. Odchylenie standardowe może opisywać zarówno całą populację, jak i konkretną próbę. Jeżeli z całej populacji wylosujemy wiele prób i dla każdej z nich policzymy średnią, to otrzymane wielkości będą się od siebie lekko różniły. Jeżeli z tych wszystkich średnich policzymy odchylenie standardowe, to otrzymamy właśnie SEM. Ponieważ średnie z kolejnych prób (podgrup interesującej nas populacj) będą sobie bliskie, to i SEM będzie mniejszy niż odchylenie standardowe, mierzące odległość od średniej konkretnych przypadków (osób).

Dwie uwagi: 1) SEM zwykle interesuje nas przy testach statystycznych - raczej nie użyjemy go w opisie naszej grupy badanej (chyba że mamy ku temu dobre powody), 2) pamiętajmy, że SEM jest mniejszy niż SD

2.3.3 Test statystyczny

Dochodzimy teraz do podstawowego z punktu widzenia praktyka pojęcia, czyli do testu statystycznego. Test statystyczny to pewna procedura, pozwalająca na podstawie zebranej próby oszacować prawdziwość pewnego stwierdzenia o populacji. Posłużmy się od razu przykładem.

Powiedzmy że interesuje nas, czy wzrost mężczyzny w Polsce jest obecnie większy niż w 1880 r. Ze źródeł literaturowych możemy przyjąć, że wzrost w 1880 r. wynosił 165,0 cm. Dla ułatwienia problemu przyjmy, że pytamy, czy mężczyźni żyjący obecnie są wyżsi niż 165,0 cm (dla zainteresowanych: ignorujemy w ten sposób niepewność danych historycznych). W definicji testu podanej wyżej mamy 4 elementy, które w naszym przykładzie są następujące

testowane stwierdzenie o populacji: wzrost mężczyzn w 2012 r. jest nie większy niż 165,0 cm,
zbieramy próbę 1000 mężczyzn (mierzymy ich wzrost) - średnia tych pomiarów to 177,9 cm,
wpisujemy wyniki pomiaru do komputera, który przeprowadza procedurę testującą,
w wyniku dowiadujemy się, że nasze stwierdzenie nie jest poparte przez zebrane dane - komputer wylicza na podstawie danych pewną liczbę (tzw. wartość p), która jest za mała abyśmy mogli to stwierdzenie przyjąć,

Zwróćmy uwagę, że nasze stwierdzenie o populacji jest trochę dziwne: zakładamy, że wzrost mężczyzn jest nie większy niż 165,0 cm, podczas gdy chcemy pokazać coś zupełnie odwrotnego. Jest to typowe podejście w biostatystyce. Przyjmujemy pewną hipotezę i staramy się ją odrzucić. Hipoteza ta nazywana jest hipotezą zerową, oznaczaną jako H0, i zgodnie z ogólnie przyjętą metodologią jest ona konserwatywna, czyli zakłada brak zmian, różnic, postępów itd. Konserwatyzm jest charakterystyczny dla nauk medycznych: nie zmienia się postępowania, póki nie ma mocnych dowodów, że taka zmiana jest korzystna i że stanowi postęp w stosunku do obecnie używanych procedur. Zwykle stosuje się również tak zwaną hipotezę alternatywną, czyli hipotezę, która pozostaje po odrzuceniu hipotezy zerowej - tę hipotezę oznacza się jako HA. W naszym przypadku jest to stwierdzenie „mężczyźni obecnie żyjący w Polsce są wyżsi niż 165,0 cm”.

Opisane tutaj podejście do testów statystycznych nie jest jedynym używanym w praktyce. Istnieją inne podejścia do tego problemu, a statystycy, matematycy i przedstawiciele innych dziedzin prowadzą zawzięte, często bardzo emocjonalne dyskusje o tym, które z podejść jest lepsze. Podejście opisane tutaj jest standardem w naukach biomedycznych.

2.3.4 Czym jest wartość p?

Zapewne wszyscy spotkaliśmy się kiedyś z mityczną “wartością p” - jest ona powszechnie używana i cytowana zarówno w literaturze naukowej jak i w mediach. Co jednak oznacza owo p?

Interpretowanie wartości p przypomina trochę chodzenie po polu minowym - jeden nierozważny krok i wylatujemy w powietrze. Za rogiem zawsze czyha jakiś statystyk, gotów udowodnić nam, że zupełnie nie rozumiemy ani metodologii statystycznej, ani podstawowych pojęć. Proszę zwrócić uwagę jak bardzo starałem się w ostatnim punkcie, żeby nic konkretnego o p nie powiedzieć!

Przyczyną tego stanu rzeczy jest fakt, że współczesna metodologia statystyczna jest mieszaniną dwóch zwalczających się podejść: brytyjskiego uczonego Ronalda Fishera i naszego rodaka, matematyka Jerzego Spławy-Neymana. Pomimo że obaj panowie darzyli siebie gorącą niechęcią i pomimo tego, że obaj uważali swoje podejścia za sprzeczne, obecne podręczniki praktycznej statystki bez słowa komentarza łączą obie teorie w jedno, tworząc taki galimatias, że nie sposób jednoznacznie zdefiniować pewnych podstawowych pojęć - jednym z nich jest wartość p.

Jak wspominaliśmy, celem naszym jest pragmatyczna próba nauczenia się korzystania ze statystyki, a nie rozumienia i interpretowania wszystkich jej niuansów i zawiłości. Podajmy więc kilka stwierdzeń, które pomogą nam użyć wartości p:

Zgodnie z Fisherem, wartość p mierzy to, jak silne mamy dowody przeciwko H0, czyli przeciwko naszemu stwierdzeniu. Im mniejsze p, tym silniejsze dowody przeciwko hipotezie zerowej. W naszym powyższym przykładzie p=0,0003, więc mamy mocne dowody na to, że mężczyźni w 2012 roku są wyżsi niż 165,0 cm (statystycy teoretyczni nie przepadają za tą interpretacją).
W testowaniu statystycznym przyjmujemy pewne wartości graniczne, po osiągnięciu których mówimy, że nasza hipoteza jest odrzucona. Najczęściej przyjętymi wartościami są 0,05 i 0,01. Czyli jeżeli przyjęliśmy wartość 0,05, to gdy komputer „wypluje” jakieś p, które jest mniejsze od tej wartości (p<0,05), mówimy, że hipoteza została odrzucona. W takie sytuacji mówimy również często, że coś jest większe od czegoś innego, że efekt jest istotny, czy że pomiędzy wielkościami istnieje związek, w zależności od testu, który wykonaliśmy.
Powyższą wartość graniczną nazywamy często poziomem istotności - ponownie, statystycy teoretyczni nie byliby w tym miejscu zachwyceni.
Wartość p odpowiada pewnemu prawdopodobieństwu. Jeżeli to prawdopodobieństwo jest małe, to znaczy, że małe są szanse, że dane potwierdzają nasze założenia. Nie można tu jednak mówić o jakichś równościach (np. “p to prawdopodobieństwo, że H0 jest prawdziwe”
- takie stwierdzenie jest błędne!).

Podsumowując, gdy komputer podaje p<0,05, mówimy o istotnym efekcie, jeżeli nie, to mówimy, że efekt jest nieistotny statystycznie.

2.3.5 Czym są przedziały ufności?

Jest jeszcze inna metoda podawania wyników testów statystycznych. Jeżeli chcemy powiedzieć coś o jakiejś wielkości, to możemy podać pewien przedział, w którym ta wielkość również się znajduje. Jeżeli inna wielkość znajdzie się w tym przedziale, to mówimy, że pomiędzy porównywanymi wielkościami (efektami itd.) nie ma istotnej różnicy. Jeżeli druga wielkość wypada poza ten przedział, to mówimy że różnica (efekt) jest. Przedział ten nazywa się przedziałem ufności i zależy od poziomu istotności opisanego powyżej. Każdy poziom istotności ma swój przedział ufności, który jednak opisuje się przez wielkość (1-poziom istotności)*100%, czyli możemy mówić np. o 95% przedziale ufności (odpowiada to poziomowi istotności, czyli wartości granicznej dla p, równemu 0,05 - obliczamy (1-0,05)*100%=95%). Podkreślmy, że przedział ufności wylicza komputer, czyli jest to pewien wynik, który uzyskamy z oprogramowania i który będziemy musieli/chcieli tylko zinterpretować.

Od razu podajmy przykład: 95% przedział ufności dla powyższego testu na to, czy mężczyźni są wyżsi niż 165,0 cm wynosi (171,1 - 184,7). Wartość 165,0 jest poza tym przedziałem, więc mówimy, że obecnie wzrost mężczyzn w Polsce jest większy niż 165,0 cm. W tym samym przypadku, 99% przedział ufności wynosi (175,6-180,2), więc na poziomie istotności 0,01 liczba 165,0 jest jeszcze dalej od od przedziału ufności.

Przedział ufności oznacza się często symbolem 95%CI, lub 99%CI - CI od confidence interval.

2.3.6 Testy parametryczne i nieparametryczne

Wielkości wartości p i szerokość przedziału ufności zależą od założeń. Jednym z najważniejszych założeń testów statystycznych używanych w naukach biomedycznych jest normalność rozkładu.

Jeżeli jesteśmy w stanie potwierdzić, że rozkład jest normalny, to zastosujemy test z grupy testów parametrycznych, jeżeli nie, to zastosujemy testy parametryczne. Rozdział Testy rozkładu opisuje jak można sprawdzić, czy rozkład jest normalny, czy nie - można to zrobić przy pomocy odpowiedniego testu statystycznego na komputerze, przy użyciu dostępnych danych

Ten punkt kończy rozdział zawierająca podstawy. Po zaznajomieniu się z tym rozdziałem można przejść bezpośrednio do rozdziału zawierającego interesujące dla Czytelnika informacje - nie trzeba zachowywać kolejności w jakiej reszta podręcznika została napisana. W niektórych przypadkach materiał będzie wymagał opanowania innego rozdziału. Informacja o tym jakie części (Mini) Podręcznika są potrzebne do zrozumienia materiału są podane na początku każdego rozdziału.

2.4 Program statystyczny: histogram i opis danych

Poniżej zamieszczony program służy rysowaniu histogramu z dostępnych danych (np. z danych zawartych w jednej kolumnie w arkuszu kalkulacyjnym) oraz liczeniu podstawowych charakterystyk, takich jak średnia, ochylenie standardowe, mediana, wartość minimalna, maksymalna oraz IQR. Aby z niego skorzystać wpisujemy dane do pierwszego pola, oddzielając liczby spacjami (można używać zarówno kropki jak i przecinka dziesiętnego: można wpisać zarówno 1,1 jak i 1.1) lub wklejamy dane z Excela bądź LibreOffice (OpenOffice) - ten diagram demonstruje jak to zrobić. W następne pole wpisujemy tytuł wykresu (który pojawi się na górze). W kolejnych dwóch polach podajemy nazwę zmiennej (np. “wzrost (cm)”) i opis osi y (np. “liczba przypadków”, “number” itd.). Potem wybieramy tylko kolor punktów na wykresie i gotowe. Pod wykresem znaleźć można tabelkę zawierającą wymienione wyżej wielkości. Program startuje z pewnymi danymi domyślnymi (odpowiadającymi przykładowi ze wzrostem mężczyzn. Pierwsze 300 wartości tego zbioru danych pobrać można pobrać w formacie Excela tutaj, a w formacie pliku tekstowego csv tutaj.

Here is a review of existing methods.