Rozdział 6 Korelacje

…

Aby zrozumieć ten rozdział należy zapoznać się z rozdziałem Podstawy. 

Korelacje to chyba jedna z najczęściej wykorzystywanych technik statystycznych. Korelacja opisuje siłę i typ związku pomiędzy dwiema zmiennymi. Siła związku opisywana jest pewną liczbą (do której zaraz wrócimy), a typ opisywany jest słowem “dodatnia” lub “ujemna” (nazywane również “pozytywna” i “negatywna”) , albo znakiem + lub -. Na przykład pomiędzy wzrostem i masą ciała istnieje dodatnia korelacja: im większy wzrost tym większa masa. Oczywiście nie zawsze będzie tak, że wyższa osoba będzie ważyła więcej, jednak ogólnie, dla dużej grupy ludzi, obserwacja ta będzie prawdziwa.

Liczbą, która opisuje jednocześnie siłę i typ korelacji jest współczynnik korelacji oznaczany często literą r. Dla każdej pary zmiennych (takich jak na przykład wzrost i masa) liczba ta zawiera się pomiędzy -1 a +1. Znak współczynnika korelacji (+/-) odpowiada typowi korelacji (dodatnia/ujemna), a jego wartość bezwzględna opisuje siłę związku - im bliżej jedynki tym silniejsza korelacja.

Na przykład w pewnej grupie ludzi współczynnik korelacji pomiędzy ich wzrostem a masą wyniósł r=0.8. Oznacza to, że związek pomiędzy masą a wzrostem był pozytywny (jak wyżej) i dość silny.

6.1 Korelacja Pearsona i korelacja Spearmana

W powszechnym użyciu są trzy typy korelacji: wg. Pearsona, Spearmana i Kendalla. Pierwszy typ jest używany najczęściej, trzeci najrzadziej. Współczynnik korelacji Pearsona mierzy siłę liniowego związku pomiędzy zmiennymi. Liniowy związek to taki, w którym punkty na wykresie rozproszeniowym dwóch badanych zmiennych układają się mniej więcej na linii prostej. Na rysunku poniżej zobaczyć możemy przykłady związku liniowego i nieliniowego.

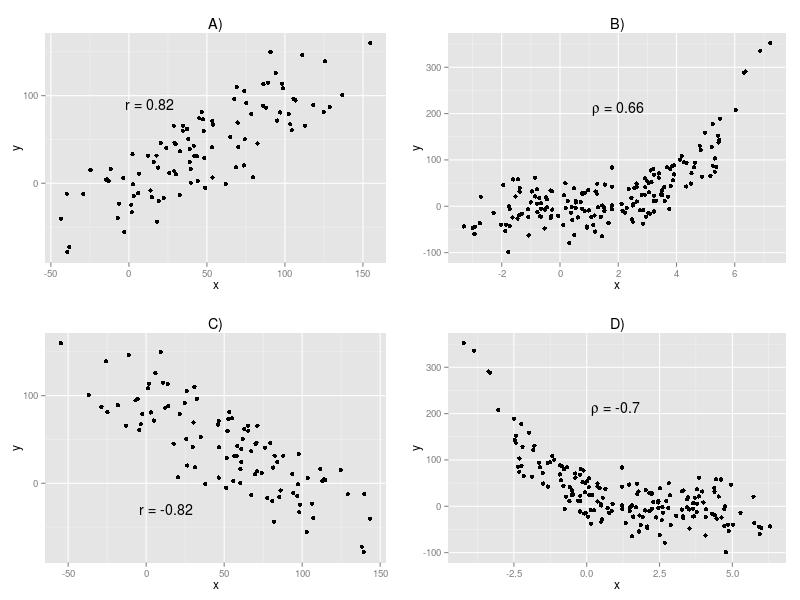
Zignorujmy na razie napisy wewnątrz rysunków i skupmy się na wzorze, w jaki układają się dane. W panelach A) i B) widać, że ze wzrostem x rośnie y i odwrotnie, gdy x maleje, maleje również y. W przypadku tych dwóch paneli korelacja jest dodatnia.

W przypadku paneli C) i D) gdy x rośnie, y maleje i odwrotnie, gdy x rośnie, y maleje. Korelacja jest ujemna.

Inną cechą widoczną na rysunkach A) i C) jest liniowość związku. Jak widać punkty układają się mniej więcej wzdłuż prostej, czego nie można powiedzieć o punktach na panelach B) i D). O zależności przedstawionej na rysunkach A) i C) powiemy, że są to zależności liniowe. Zależności na rysunkach C) i D) są nieliniowe. Aby zbadać siłę liniowego związku używamy techniki korelacji Pearsona. Badając zależności nieliniowe, użyjemy korelacji Separmana (ewentualnie Kendalla). Wynikiem uzyskanym z analizy siły związku metodą korelacji Pearsona jest wartość r, która może przyjmować wartości dodatnie (korelacja dodatnia) i ujemne (korelacja ujemna). Im wyższa dodatnia wartość r, tym silniejszy jest związek dodatni. Im niższa wartość tym silniejszy jest związek ujemny. Wartości w okolicach zera oznaczają zazwyczaj brak związku. Dokładnie to samo powiedzieć można o korelacji Spearmana, z tym że parametrem opisującym siłę związku jest tutaj ρ (rho), przyjmujące wartości pomiędzy -1 a +1 (identycznie jak r).

W tym miejscu warto poczynić następującą uwagę: Dane, dla których korelacja Pearsona jest bliska 1 bądź -1 układają się w wyraźną linię prostą. W przypadku korelacji Spearmana bliskiej 1 lub -1 dane układają się wzdłuż pewnej rosnącej lub malejącej krzywej. W przypadku obu typów korelacji, wartość bliska 0 oznacza, że dane rozkładają się w chmurę o nieokreślonym kształcie.

6.2 Testy statystyczne dla korelacji

Do tej pory zajmowaliśmy się kierunkiem i siłą związku. W tym momencie chcielibyśmy przetestować nasze wyniki, czyli powiedzieć, na ile są one istotne statystycznie. Zacząć musimy oczywiście od postawienia pewnej hipotezy zerowej, którą będziemy w stanie odrzucić. Naszą hipotezą jest “zmienne nie mają ze sobą żadnego związku i współczynnik korelacji (r lub ρ) jest równy 0”. Oczywiście dla realnych danych zawsze z obliczeń praktycznie zawsze otrzymamy wynik różny od zera, a nasz test pozwoli nam powiedzieć, czy dla tych danych, którymi się posługujemy różnica ta jest wystarczająco duża, aby móc przyjąć, że obserwowany związek jest prawdziwy i nie jest jedynie kwestią przypadku. Oczywiście, mając w pamięci dyskusję w rozdziale Podstawy słowo “prawdziwy” bierzemy w duży cudzysłów.

W przypadku obu typów korelacji mamy do dyspozycji testy statystyczne, choć nie mają one konkretnych nazw, tak jak np. test t czy ANOVA - po prostu test istotności korelacji Pearsona lub test istotności korelacji Spearmana (choć gdybyśmy poszukali głębiej, to znaleźlibyśmy konkretne nazwy tych testów). Podobnie jak poprzednio, jeżeli wartość p uzyskana w tym teście jest mniejsza niż pewna z góry przyjęta wartość (standardowo 0.05), to odrzucamy hipotezę zerową. Przypomnijmy, że w naszym przypadku hipoteza zerowa (H0), to “nie ma związku pomiędzy zmiennymi”, więc odrzucamy stwierdzenie o braku związku i przyjmujemy, że związek taki istniej. Jeżeli p>0.05 to przyjmujemy, że nie mamy podstaw do odrzucenia H0 i stwierdzamy, że pomiędzy zmiennymi nie ma związku.

Przeanalizujmy następujący przyład. Wszystkich nas interesuje, czy większa głowa oznacza tęższy umysł.W 1991 roku sprawdzono, czy wielkość mózgu (zmierzona przy pomocy techniki MRI) ma związek z inteligencją - pełną analizę można znaleźć tutaj. Wielkość mózgu mierzona była przez liczbę niezerowych pikseli na obrazach MRI. W tym pliku znaleźć można dane dotyczące 20 mężczyzn biorących udział w badaniu w formacie csv (plik Excela znajduje się tutaj). Dane analizujemy przy pomocy wybranego programu statystycznego (na przykład tego, który znajduje się na dole tej strony) i dla korelacji Pearsona otrzymujemy r=0.50 przy p=0.025, a dla korelacji Spearmana ρ=0.62 przy p=0.003. Jak widać korelacja Spearmana jest silniejsza i wartość p w tym rodzaju korelacji jest mniejsza - nie jest to dziwne, biorąc pod uwagę kształt wykresu (patrz poniżej - program statystyczny).

Wyniki te moglibyśmy analizować dalej i poddać interpretacji, ale w tym (mini) podręczniku poprzestaniemy na stwierdzeniu, że w omawianym badaniu stwierdzono dodatni związek pomiędzy wielkością mózgu, a współczynnikiem inteligencji.

6.3 Program statystyczny: korelacje Pearsona i Spearmana

Poniższy program rysuje wykres zależności dwóch zmiennych i oblicza współczynnik korelacji. W pierwszym polu zaznaczamy, czy chodzi nam korelację Pearsona czy Spearmana. W następnym polu wklejamy lub wpisujemy dane, które odkładane będą na osi x (czyli np. wielkość mózgu) , a w kolejnym dane, które odkładane będą na osi y (czyli np. wynik testu inteligencji). Można używać zarówno kropki jak i przecinka dziesiętnego: można wpisać zarówno 1,1 jak i 1.1. Ten diagram opisuje proces przeklejania danych z Excela lub LibreOffice (OpenOffice). W kolejnym polu wpisujemy opis osi x i y. Na koniec wybieramy kolor punktów na wykresie.