Kulki i łańcuchy (Markova)

Na Quora pojawiło się kolejne bardzo ciekawe pytanie związane z rachunkiem prawdopodobieństwa:

W pudełku A znajduje się 100 czerwonych kulek, a w pudełku B 100 niebieskich. Co sekundę wybieram losowo jedną kulkę z każdego pudełka i je wymieniam. Jaki jest oczekiwany czas do uzyskania stanu 50/50?

Alternatywnie: jak długo trzeba czekać aż system kulki/pudełka przejdzie od stanu minimalnej entropii do maksymalnej?

Odpowiedzią nie jest 50 sekund, bo w pewnym momencie można wybrać kulkę wcześniej już przesuniętą i odłożyć ją do pudełka startowego.

Moją odpowiedź na Quora można znaleźć tutaj (UPDATE 2021: oryginał mojej odpowiedzi już niedostępny - skasowałem konto na Quora), poniżej tłumaczenie na polski.

To jest jedno z tych pytań, które choć wyglądają na proste, okazują się być cholernie trudne.

OK! Zaczynamy.

Na początek wyrażę pytanie w innymi słowami. Mamy dwa pudełka, jedno z nich, (1), zawiera 100 czerwonych kulek, a drugie (2) 100 niebieskich kulek. Co sekundę wkładamy lewą rękę do pudełka 1 i losowo wybieramy kulkę. Jednocześnie prawą rękę wkładamy do pudelka 2 i również losujemy. To co wylosujemy przekładamy do drugiego pudełka, czyli kulka z prawej ręki idzie do pudełka 1 a kulka z lewej ręki idzie do pudełka 2.

Pudełka są swoimi lustrzanymi odbiciami. Jeżeli w pudełku 1 mamy \(n\) czerwonych kulek to na pewno w pudełku drugim jest \(n\) niebieskich kulek. Prawdopodobieństwo wylosowania czerwonej kulki z pudełka 1 zależy jedynie od bieżącej zawartości tego pudełka. Jeżeli w pudelku 1 mamy 23 niebieskie kulki to prawdopodobieństwo nie zależy od tego jak te kulki się tam dostały (w ilu ruchach). To pachnie łańcuchem Markova … .

Spróbujmy więc stworzyć reprezentację naszego eksperymentu jako łańcucha Markowa. Skoncentrujmy się jedynie na pudełku 1 - pudełko 2 jest lustrzanym odbiciem (dodatkowo, jego obecność pomaga nam zliczać prawdopodobieństwa, ale nie musi się ono pojawiać w konkretnych obliczeniach). Stanem pudełka 1 nazwiemy liczbę niebiestkich kulek w nim zawartych, czyli na przykład stan (0) będzie oznaczał “w pudełu 1 nie ma niebiestkich kulek”, stan (35) oznacza “w pudełku pierwszycm jest 35 niebieskich kulek”. Rozpocznijmy od stanu (0).

W stanie (0) prawdopodobieństwo przejścia do stanu (1) wynosi \(1\). Faktycznie, prawa ręka wylosuje niebieską kulkę w każdej sytuacji. Ze stanu (1) możemy przejść do stanu (2), zostać w stanie (1) albo powrócić do stanu (0).

Prawdopodobieństwo przejścia do stanu (2) jest równe prawdopodobieństwu wylosowania jednej czerwonej kulki spośród 99 czerwonych kulek ORAZ jednej niebieskies spośród 99 niebieskich i 1 czerwonej. Możemy więc stwierdzić, że prawdopodobieństwo przejścia do stanu (2) wynosi \(\left(\frac{99}{100}\right)^2\).

Prawdopodobieństow pozostania w stanie (1) równe jest prawdopodobieństwu wylosowania czerwonej kulki z pudełka 1 oraz czerwonej z pudełka 2 LUB niebieskiej z pudełka 1 oraz niebieskiej z pudełka 2. Biorąc pod uwagę to, ile kulek mamy w każdym pudełku uzyskujemy prawdopodobieństwo

\[p=\frac{1}{100}\cdot\frac{99}{100}+\frac{99}{100}\cdot\frac{1}{100} = 2\cdot \frac{1}{100}\cdot\frac{99}{100}.\] Prawdopodobieństwo powrotu do stanu (0) jest równe prawdopodobieństwu wylosowania niebieskiej kulki z pudełka 1 (jedynej niebieskiej wśród 100 kulek) ORAZ jednej czerwonej z pudełka 1, co daje nam \(\left(\frac{1}{100}\right)^2\).

Wykonując podobne obliczenia dla stanu (2) możemy narysować pierwsze trzy stany naszego łańcucha Markowa.

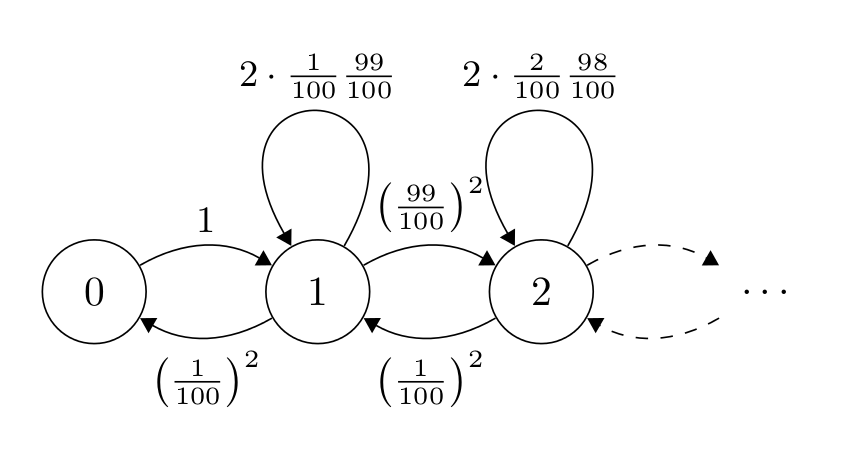
Pierwsze trzy stany łańcucha Markova

Możemy teraz uogólnić powyższe prawdopodobiestwa dla dowolnego stanu w łańcuchu. Przyjmijmy nstępujące nazewnictwo: prawdopodobieństwo przejścia ze stanu (\(i\)) do następnego stanu nazwiemy \(b_i\) a prawdopodobieństwo przejścia do poprzedniego staniu \(d_i\). Nasz łańcuch Markowa jest przykładem łańcucha typu procesu “urodzin i śmierci”, lub po angielsku “birth-death processes” (w pudełku 1 niebieska kulka się “rodzi” lub “umiera”) - stąd właśnie “b” i “d”. Załużmy, że liczba kulek w pudełku \(N\) jest parzysta. Łatwo teraz uogólnić nasze powyższe obliczenia prawdopodobieństw:

\[b_i = \left(\frac{N-i}{N}\right)^2\] \[d_i = \left(\frac{i}{N}\right)^2\] W stanie (\(i\)) możemy pójść w prawo lub lewo albo pozostać w tym stanie, więc prawdopodobieństwo pozostania można uprościć do \(1-b_i-d_i\).

Czyli pełny łańcuch Markowa wygląda następująco:

Pełny łańcuch Markova.

Przyjmimy następującą notację: \(t_i\) jest czasem potrzebnym żeby dojść od stanu (0) do stanu (\(\frac{N}{2}\)) PO RAZ PIERWSZY. Gdy już dotrzemy do (\(\frac{N}{2}\)) to się zatrzymamy, lub, mówiąc inaczej, pozostaniemy tam na zawsze. Standardowym trikiem w takich sytuacjach jest przekształcenie docelowego stanu na stan absorbujący, czyli taki, z którego nie można się wydostać. Można to zrobić domykając pętlę na (\(\frac{N}{2}\)) z prawdopodobieństwem 1 i ustawienie \(d_{\frac{N}{2}}=0\). W rezultacie otrzymujemy następujący łańcuch Markowa:

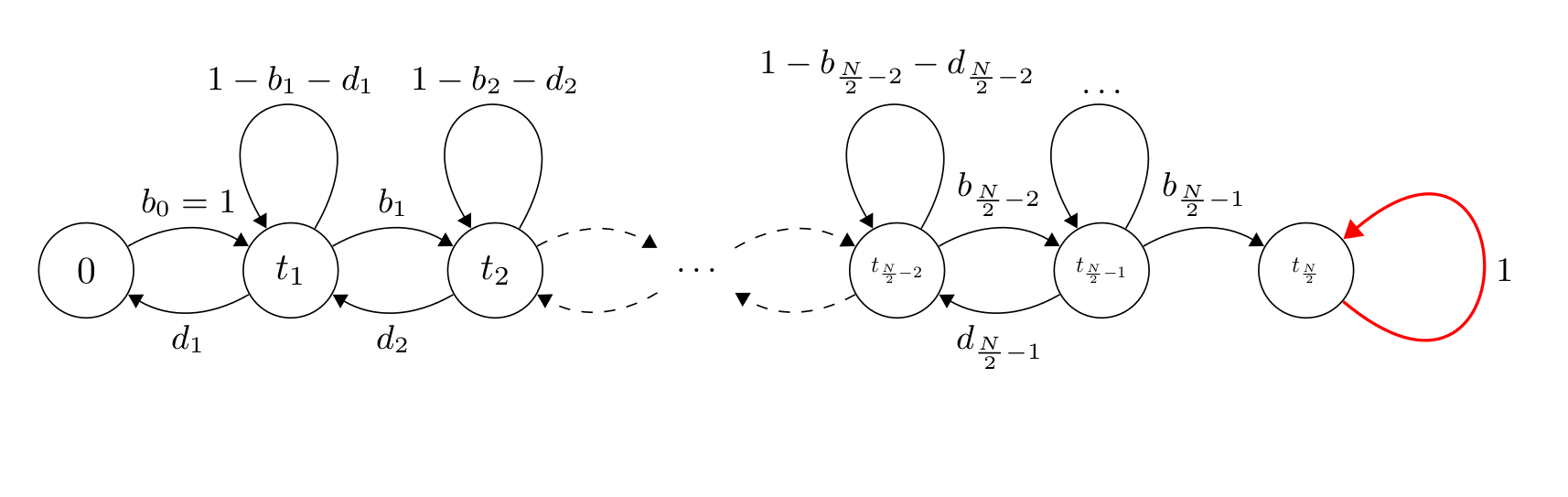
Łańcuch Markova absorbujący przy (\(\frac{N}{2}\)).

Załóżmy że jesteśmy w stanie (\(i\)). Możemy przejść dalej do stanu (\(i-1\)), skąd oczekiwany czas do absorbcji wynosi, zgodnie z naszą definicją, \(t_{i-1}\), lub do stanu (\(i+1\)), skąd oczekiwany czas do absorbcji wynosi \(t_{i+1}\), lub pozostać w stanie (\(i\)), skąd oczekiwany czas wynosi \(t_{i}\). Tak więc czas, którego potrzebujemy aby dotrzeć do (\(\frac{N}{2}\)) z (\(i\)) wynosi 1 (dla pierwszego skoku) plus wartość oczekiwana pozostałych stanów:

\[ t_i = 1 + b_{i}t_{i+1} + d_{i}t_{i-1} + (1-b_i-d_i)t_i\]. Zauważmy również, że stany (\(0\)) i (\(\frac{N}{2}\)) są różne gdyż

\[ t_0 = 1 + t_1 \] a, ponieważ \(t_{N/2}=0\) (potrzebujemy zero czasu żeby dojść od (\(\frac{N}{2}\)) do (\(\frac{N}{2}\)) po raz pierwszy)

\[t_{\frac{N}{2}-1} = 1 + d_{\frac{N}{2}-1}t_{\frac{N}{2}-2} + (1-b_i-d_i)t_{\frac{N}{2}-1}\] Uwierzcie lub nie, ale już skończyliśmy. Ostatnie trzy równania opisują prosty układ równań, który można w prosty sposób rozwiązać - jedynym problemem może być jego rozmiar. W przypadku oryginalnego pytania ze 100 kulkami będziemy mieli układ 50 prostych równań, który można rozwiązać dokładnie. Można to zrobić ręcznie (jeżeli ktoś ma tyle czasu) lub przy użyciu oprogramowania. Poniżej prosty kod w maximie

b(i):= ((100-i)/100)^2;
d(i):= (i/100)^2;
e0: t0 - t1 = 1;
e1: t1*(b(1) + d(1)) = 1 + b(1)*t2 + d(1)*t0;
e2: t2*(b(2) + d(2)) = 1 + b(2)*t3 + d(2)*t1;
e3: t3*(b(3) + d(3)) = 1 + b(3)*t4 + d(3)*t2;
e4: t4*(b(4) + d(4)) = 1 + b(4)*t5 + d(4)*t3;
e5: t5*(b(5) + d(5)) = 1 + b(5)*t6 + d(5)*t4;
e6: t6*(b(6) + d(6)) = 1 + b(6)*t7 + d(6)*t5;
e7: t7*(b(7) + d(7)) = 1 + b(7)*t8 + d(7)*t6;
e8: t8*(b(8) + d(8)) = 1 + b(8)*t9 + d(8)*t7;
e9: t9*(b(9) + d(9)) = 1 + b(9)*t10 + d(9)*t8;
e10: t10*(b(10) + d(10)) = 1 + b(10)*t11 + d(10)*t9;
e11: t11*(b(11) + d(11)) = 1 + b(11)*t12 + d(11)*t10;
e12: t12*(b(12) + d(12)) = 1 + b(12)*t13 + d(12)*t11;
e13: t13*(b(13) + d(13)) = 1 + b(13)*t14 + d(13)*t12;
e14: t14*(b(14) + d(14)) = 1 + b(14)*t15 + d(14)*t13;
e15: t15*(b(15) + d(15)) = 1 + b(15)*t16 + d(15)*t14;
e16: t16*(b(16) + d(16)) = 1 + b(16)*t17 + d(16)*t15;
e17: t17*(b(17) + d(17)) = 1 + b(17)*t18 + d(17)*t16;
e18: t18*(b(18) + d(18)) = 1 + b(18)*t19 + d(18)*t17;
e19: t19*(b(19) + d(19)) = 1 + b(19)*t20 + d(19)*t18;
e20: t20*(b(20) + d(20)) = 1 + b(20)*t21 + d(20)*t19;
e21: t21*(b(21) + d(21)) = 1 + b(21)*t22 + d(21)*t20;
e22: t22*(b(22) + d(22)) = 1 + b(22)*t23 + d(22)*t21;
e23: t23*(b(23) + d(23)) = 1 + b(23)*t24 + d(23)*t22;
e24: t24*(b(24) + d(24)) = 1 + b(24)*t25 + d(24)*t23;
e25: t25*(b(25) + d(25)) = 1 + b(25)*t26 + d(25)*t24;
e26: t26*(b(26) + d(26)) = 1 + b(26)*t27 + d(26)*t25;
e27: t27*(b(27) + d(27)) = 1 + b(27)*t28 + d(27)*t26;
e28: t28*(b(28) + d(28)) = 1 + b(28)*t29 + d(28)*t27;
e29: t29*(b(29) + d(29)) = 1 + b(29)*t30 + d(29)*t28;
e30: t30*(b(30) + d(30)) = 1 + b(30)*t31 + d(30)*t29;
e31: t31*(b(31) + d(31)) = 1 + b(31)*t32 + d(31)*t30;
e32: t32*(b(32) + d(32)) = 1 + b(32)*t33 + d(32)*t31;
e33: t33*(b(33) + d(33)) = 1 + b(33)*t34 + d(33)*t32;
e34: t34*(b(34) + d(34)) = 1 + b(34)*t35 + d(34)*t33;
e35: t35*(b(35) + d(35)) = 1 + b(35)*t36 + d(35)*t34;
e36: t36*(b(36) + d(36)) = 1 + b(36)*t37 + d(36)*t35;
e37: t37*(b(37) + d(37)) = 1 + b(37)*t38 + d(37)*t36;
e38: t38*(b(38) + d(38)) = 1 + b(38)*t39 + d(38)*t37;
e39: t39*(b(39) + d(39)) = 1 + b(39)*t40 + d(39)*t38;
e40: t40*(b(40) + d(40)) = 1 + b(40)*t41 + d(40)*t39;
e41: t41*(b(41) + d(41)) = 1 + b(41)*t42 + d(41)*t40;
e42: t42*(b(42) + d(42)) = 1 + b(42)*t43 + d(42)*t41;
e43: t43*(b(43) + d(43)) = 1 + b(43)*t44 + d(43)*t42;
e44: t44*(b(44) + d(44)) = 1 + b(44)*t45 + d(44)*t43;
e45: t45*(b(45) + d(45)) = 1 + b(45)*t46 + d(45)*t44;
e46: t46*(b(46) + d(46)) = 1 + b(46)*t47 + d(46)*t45;
e47: t47*(b(47) + d(47)) = 1 + b(47)*t48 + d(47)*t46;
e48: t48*(b(48) + d(48)) = 1 + b(48)*t49 + d(48)*t47;
e49: t49*(b(49) + d(49)) = 1 + b(49)*0 + d(49)*t48; 
algsys([e0, e1, e2, e3, e4, e5, e6, e7, e8, e9, e10, e11, e12, e13, e14, e15, e16, e17, e18, e19, e20, e21, e22, e23, e24, e25, e26, e27, e28, e29, e30, e31, e32, e33, e34, e35, e36, e37, e38, e39, e40, e41, e42, e43, e44, e45, e46, e47, e48, e49], [t0, t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12, t13, t14, t15, t16, t17, t18, t19, t20, t21, t22, t23, t24, t25, t26, t27, t28, t29, t30, t31, t32, t33, t34, t35, t36, t37, t38, t39, t40, t41, t42, t43, t44, t45, t46, t47, t48, t49])
[[t0=163.2766635885575,t1=162.2766635885575,t2=161.2562575075453,t3=160.2145996957665,t4=159.1507911167139,t5=
158.0638747823753,t6=156.9528306928064,t7=155.8165702143972,t8=154.6539298208901,t9=153.46366410903,t10=
152.2444379862597,t11=150.99481791067,t12=149.7132620428318,t13=148.3981091444629,t14=147.0475660291472,t15=
145.659693334366,t16=144.2323893404108,t17=142.7633715084306,t18=141.250155344482,t19=139.69003011588,t20=
138.0800308463288,t21=136.4169058919819,t22=134.6970792448313,t23=132.9166065135327,t24=131.0711232828265,t25=
129.155784234889,t26=127.1651910073404,t27=125.0933062334502,t28=122.9333505194014,t29=120.6776782046224,t30=
118.3176265448864,t31=115.8433313420778,t32=113.2434998592172,t33=110.5051288733934,t34=107.6131515948098,t35=
104.549991417114,t36=101.2949923123383,t37=97.82368400184286,t38=94.10682306027867,t39=90.10912607806777,t40=
85.78757350888132,t41=81.08910570035403,t42=75.94744399793103,t43=70.27862971639888,t44=63.97464768914345,t45=
56.89412817231738,t46=48.84849114039249,t47=39.58080665494906,t48=28.73270589726143,t49=15.79112892029682]]

(linijki 61–77 zawierają rozwiązanie). Czyli czas potrzebny do wyrównania liczby kulek (gdy jest po 50 kulek w każdym pudełku) wynosi \(t_0=163.277\). Jako bonus otrzymaliśmy wszystkie oczekiwane czasy z pozostałych stanów, które możemy dalej analizować.

Jeszcze jedna rzecz. Te obliczenia wyglądają przekonująco, ale skąd wiemy, że nie zrobiliśmy błędu? Skąd wiadomo, że takie podejście ma sens? W takim przypadku dobrym rozwiązaniem jest zawsze symulacja. Napiszmy więc funkcję w R, która zysymuluje eksperyment wiele razy i policzy średnie czasy dla różnych stanów. Ta symulacja nie może używać łańcuchów Markowa - musi być to prosta wymiana kulek pomiędzy pudełkami. Napiszy więc funkcję przyjmującą numer stanu i zwracającą średni czas do uzyskania stnu 50/50.

set.seed(777)
t_n <- function(n){
  accumulator <- c()
  N <- 1000000
  for (i in 1:N){
    boxA <- c(rep(1,100-n), rep(0,n))
    boxB <- c(rep(0,100-n), rep(1,n))
    number <- 0
    while(sum(boxA)>50){
      drawA <- sample(seq(1,100),1)
      drawB <- sample(seq(1,100),1)
      intermediateA <- boxA[drawA]
      intermediateB <- boxB[drawB]
      boxA[drawA] <- intermediateB
      boxB[drawB] <- intermediateA
      number <- number+1
    }
    accumulator <- c(accumulator, number)
  }
  print(mean(accumulator))
}

Policzmy \(t_0\) i, powiedzmy, \(t_{45}\) - może to zabrać dłuższą chwilę - potrzebujemy dać wystarczająco dużo czasu łańcuchowi, żeby mógł odwiedzić różne stany.

t_n(0)
t_n(45)

Czyli rozwiązanie algebraiczne jest prawidłowe.

Ostatnia uwaga: jestem na 100% przekonany, że można wyprowadzić wyrażenie na oczekiwany czas w postaci zamkniętej. Istnieje obszerna literatura dotycząca rozwiązywania tego typu równań i gdybym miał jeszcze dwa dni do roztrwonienia, to na pewno bym je wyprowadził (podobnie jak każda inna osoba, która poświęciłaby temu problemowi czas i energię).

Kod skryptów użytych w tym wpisie (tex, maxima, R) dostępny jest tutaj: https://github.com/jaropis/quora_codes/tree/master/50_50_balls