Rozdział 7 Regresja liniowa

Aby zrozumieć ten rozdział należy zapoznać się z rozdziałem Podstawy.

Z regresją liniową spotkał się każdy, kto choć otarł się o statystykę - jest to najczęściej i najchętniej używana technika, służąca do modelowania związku pomiędzy dwiema (lub więcej) zmiennymi. No właśnie: modelowania …

Ten poważnie brzmiący termin wyraża prosty cel: chcemy opisać o ile zmienia się jedna wielkość przy zmianie drugiej o jednostkę. Czyli na przykład model dla zależności masy ciała od wzrostu mógłby wyglądać następująco: ze zmianą wzrostu o 1 cm masa zwiększa się o 250g. Przyjrzyjmy się bliżej temu modelowi. Druga wielkość, masa ciała, w naszym modelu zależy od pierwszej, czyli od wzrostu. Żeby powiedzieć o ile wzrośnie masa, musimy znać zmianę wzrostu. Z tego powodu wielkość ta nazywa się zmienną zależną. Pierwszą wielkość, czyli wzrost, nazywamy zmienną niezależną. Warto zwrócić uwagę na stwierdzenie, że masa jest zmienną zależną w naszym modelu. Moglibyśmy zapisać inny model, w którym zmienną niezależną byłaby masa, a zmienną zależną wzrost. Z przyczyn matematycznych te modele nie są swoimi prostymi odwrotnościami (typu: jeżeli na 1cm wzrostu masa rośnie o 250 g, to na 1g masy wzrost zmienia się o 1/250 cm - tak nie jest).

7.1 Historia

Nazwa regresja została wprowadzona przez wielkiego Francisa Galtona, którego zaintrygował fakt, że synowie wysokich ojców są średnio niżsi niż ojcowie, a synowie niskich ojców są średnio wyżsi od swoich ojców (przepraszam za wielokrotne powtórzenie słowa ojciec, ale precyzja jest ważniejsza niż styl). Innymi słowy, wzrost synów ojców wyjątkowo wysokich i wyjątkowo niskich jest bliższy średniej z populacji niż wzrost tychże ojców. Galton nazwał to zjawisko regresją do przeciętnej (regression to mediocrity), a do jego zbadania zbudował aparat pojęciowy i matematyczny, którego używamy do dzisiaj. Osoby bardziej zainteresowane matematyczną stroną statystyki chętnie przeczytają oryginalny tekst, który można znaleźć pod tym adresem.

W chwili obecnej nie używamy już słowa regresja w takim znaczeniu jak Galton, można nawet powiedzieć, że jest mylące. Z przyczyn historycznych trudno oczekiwać, że zostanie ono zastąpione innym słowej, choć w ostatnich latach coraz większą popularność zdobywa słowo model (np. liniowy, nieliniowy).

7.2 Przykład

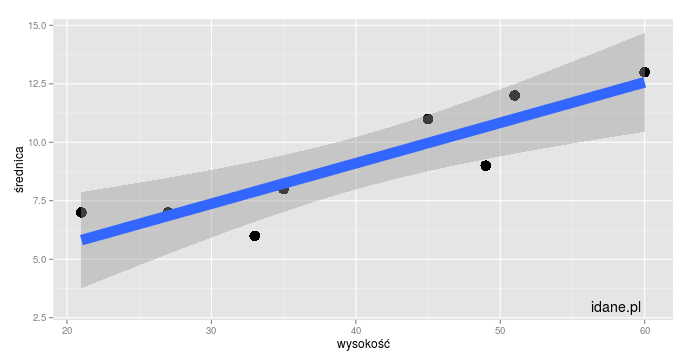
Żeby ilościowo zrozumieć regresję liniową prześledźmy szczegółowo konkretny przykład. Tym razem dla odmiany nie użyjemy przykładu z medycyny, ale z biologii. Załóżmy, że mamy do dyspozycji pomary wysokości i średnicy młodych drzew - dane w formacie Excela można pobrać tutaj a w formacie csv tutaj. Zbudujmy model zależności średnicy drzewa od wysokości drzewa - rysunek przedstawiony jest poniżej.

Po wklejeniu danych do programu znajdującego się na dole strony uzyskamy kilka różnych wyników. Najbardziej interesuje nas współczynnik kierunkowy, króry w naszym przypadku wynosi 0.17. Oznacza to, że przy wzroście wysokości drzewa o 1 cm średnica średnio zwiększy się o 0.17 cm. Liczbę tę nazywamy często współczynnikiem regresji liniowej, lub nachyleniem prostej, gdyż faktycznie osoby mające pewne doświadcznie w algebrze i geometrii rozpoznają w niej współczynnik kierunkowy prostej.

Warto zwrócić uwagę, że współczynnik regresji może być również ujemny. Na przkład w badaniu zależności liczby włosów na głowie w grupie osób w wieku od 30 do 100 lat moglibyśmy otrzymać wynik -12000/rok, czyli z każdym rokiem liczba włosów spada, co wyrażone jest właśnie ujemnym współczynnikiem regresji.

Druga liczba dostępna w wynikach działania programu to tzw. Intercept, czyli punkt przecięcia z osią zależnych. Trochę bliżej liczbę tę zinterpretujemy poniżej; tutaj napiszemy jedynie, że tę liczbę musimy dodać do każdego wyniku, który wyliczamy z modelu (patrz poniższe obliczenia).

7.3 Przykład

Do czego może się nam taki model przydać? Powiedzmy, że interesuje nas jaką w przybliżeniu średnicę ma drzewo o wysokości 30 cm. Wśród naszych danych drzewa o takiej wysokości nie mamy - mamy drzewo o wysokości 27 cm, mamy 33 cm, ale średnicę drzewa o wysokości 30 cm możemy co najwyżej oszacować z modelu. Aby to obliczyć mnożymy 30*0,17 i dodajemy Intercept, czyli 2,19. \\[ 30\\cdot0{,}17+2{,}19 = 7{,}29 \\\] Czyli nasz model przewiduje, że średnia średnica drzewa o wysokości 30 cm wynosi 7,29 cm. 30 cm jest “wewnątrz (inter)” naszych danych (pomiędzy nimi), więc przewidywanie wartości średnicy w tym przypadku nazywa się interpolacją. Jeżeli wartość jest mniejsza lub większa niż pozostałe wartości, czyli jest “poza (extra)” analizowanym przedziałem, to proces nazywa się extrapolacją.

7.4 Statystyka

Gdyby przyjrzeć się technicznej/matematycznej stronie regresji liniowej (czego oczywiście robić nie będziemy), to okaże się, że obliczenia wykonane do tej pory nie miały nic wspólnego ze statystyką, czyli z metodologią opisaną w rozdziale Podstawy - były to czyste obliczenia numeryczne.

Żeby zacząć obliczenia statystyczne musimy zdefiniować

hipotezę zerową oraz przeprowadzić test statstyczny w celu jej odrzucenia.

Hipotezą zerową w naszym przypadku jest: współczynnik regresji nie jest istotnie różny od zera, czyli ze zmianą zmiennej niezależnej nic nie dzieje się ze zmienną zależną. Dodatkowo (i w związku z tym), linia regresji jest “płaska” - nie idzie istotnie ani do góry, ani w dół. Przypadek taki przedstawiony jest na rysunku 2.

Dlaczego za każdym razem napisałem “istotnie różny”? Ponieważ zwykle przypadek sprawia, że wyliczony współczynnik jest różny od zera - jest albo trochę powyżej zera, albo trochę poniżej. Zadaniem naszego testu statystycznego jest stwierdzenie, czy ta różnica jest istotna, czy może można przyjąć, że w praktyce wynik jest po prostu zerem.

W naszym przykładzie otrzymaliśmy wynik p=0,003374, czyli uzyskany współczynnik regresji (0,17) jest istotnie statystycznie różny od zera.

7.5 Uwagi o stosowalności regresji liniowej

Na koniec, zanim przejdziemy do programu statystycznego, przedyskutujemy krótko stosowalność regresji liniowej, czyli warunki, w których stosowanie regresji liniowej, a być może co ważniejsze, interpretowanie uzyskanej wartości p ma sens.

Zmienna zależna musi mieć rozkład normalny. Warunek ten nie jest wcale tak oczywisty, na jaki wygląda. Tak naprawdę chodzi o to, żeby po odjeciu modelu od uzyskanych wartości otrzymać rozkład normalny. W praktyce warto zastanowić się, czy naszym zdaniem rozkład normalny ma sens w badanym przypadku i jeżeli odpowiedź brzmi “tak”, zastosować po prostu regresję liniową.
Nie można zbytnio ekstrapolować wyniku modelu. Jeżeli przeprowadzimy analizę przy pomocy regresji liniowej np. zależności wzrost od wieku, to ekstrapolowanie wyników uzyskanych dla przedziału wiekowego, powiedzmy 10-15 lat, do wieku 60 lat może nam dać wzrost rzędu kilometra. Jest to oczywiście bez sensu i wynika z nieuprawnionego założenia, że dynamika wzrostu od 15 do 60 roku życia nie różni się niczym od dynamiki w analizowanym przedziale. Nieuprawnione ekstrapolacje są częste w środkach masowego przekazu i w polityce - świetnie nadają się do straszenia lub napędzania koniunktury. Bardzo dobrym przykładem są artykuły w prasie nakręcające Polaków do kupowania nieruchomości przed krachem roku 2009. Przewidywano wtedy ile będą kosztowały nieruchomości z 5 lat i argumentowały, że jeżeli teraz się czegoś nie kupi, to za niedługo ceny dojdą do takiej wartości, że nigdy nie będzie nas stać na mieszkanie. Rzeczywistość szybko zweryfikowała tę nieuprawnioną ekstrapolację.

Poniżej zamieszczam program statystyczny do obliczania parametrów regresji liniowej i rysowania jej wyniku.