Zrób sobie generator

Niedawno tak się złożyło, że miałem do dyspozycji funkcję gęstości prawdopodobieństwa i musiałem zrobić sobie generator liczb losowych na jej podstawie. Zadanie to jest zaskakująco proste do zaimplementowania w R, więc postanowiłem napisać o tym krótki artykuł. Żeby uatrakcyjnić i zadanie, postarałem się wkomponować ten problem w proste zadanie na obliczenie rozkładu aposteriori z dziwacznego rozkładu apriori. Jeżeli przyszliście tutaj po kod R i teorię, to kliknijcie tutaj (link), jeżeli chcecie przeczytać rozwiązanie fajnego problemu, czytajcie dalej.

Przechodzimy teraz do skonstruowania generatora. W teorii prawdopodobieństwa możemy znaleźć następujące twierdzenie:

Jeżeli zmienna losowa \(X\) ma ciągłą dystrubuantę \(F_X(x)\) i zdefiniujemy zmienną losową \(Y = F_X(x)\), to \(Y\) ma rozkład jednorodny w przedziale \([0,1]\).

Załóżmy chwilowo, że \(F_X(x)\) jest rosnąca (czyli w żadnym miejscu nie jest stała¹). Wtedy żeby wygenerować zmienną losową z tego rozkładu wystarczy wylosować liczbę \(u\) z rozkładu jednorodnego i rozwiązać równanie \(u = F(x)\) ze względu na \(x\).

Z rozkładu prawdopodobieństwa w naszym zadaniu możemy policzyć dystrubuantę (CDF): \[ F_Q(q) = \left\{\begin{array}{l} 0\;\; dla \;\;q\in (-\infty, 0)\\ \int_0^{q}f(t)dt = \int_0^{q}3t^2 dt = q^3\;\; dla\;\; q\in [0, 1]\\ 1\;\; dla\;\; q\in (1, \infty) \end{array}\right. \]

Ponieważ znajdujemy się w przedziale \([0,1]\)¹ nie będziemy komplikować i od razu zdefiniujemy funkcję

myGenerator <- function(number, invTransFunction)
  invTransFunction(runif(number))

gdzie number to liczba liczb losowych do wygenerowania a invTransFunction to funkcja \(F^{-1}_X(u)\).

W naszym przypadku

invTransFunction <- function(y)
  (y)^(1/3)

Sprawdźmy teraz nasze obliczenia rysując teoretyczny wykres rozważanej gęstości prawdopodobieństwa i histogram wykonany przez nasz generator:

oldpar <- par(mfrow = c(1,2))
curve(3*x^2, from = 0, to = 1, ylim = c(0,3), lwd = 4, col = "red")
hist(myGenerator(10000000, invTransFunction), 
     prob = T, 
     breaks = 1000, 
     main = "", 
     col = "red")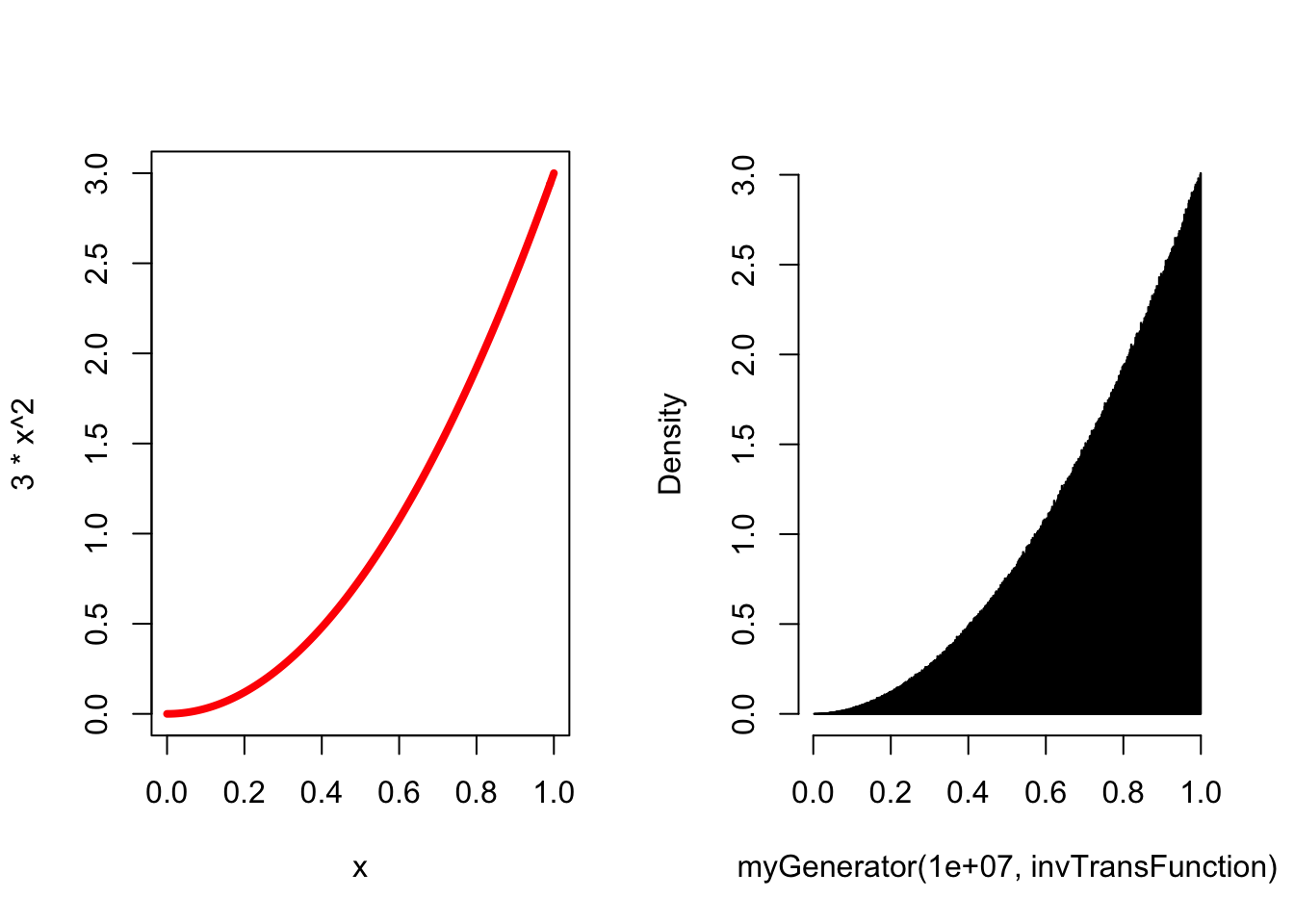

Spróbujmy teraz wykonać analityczne obliczenia - zaczynamy od \(P(A)\). Nie od razu widać, jak można to prawdopodobieństwo policzyć. Gdybyśmy jednak wiedzieli jaka liczba \(q\) została wylosowana, to z całą pewnością prawdopodobieństwo wylosowania reszki wynosiłoby \(q\). Stwierdzenie “gdybyśmy znali \(q\)” sugeruje prawdopodobieństwo warunkowe. Ubierzmy powyższe słowa w notację matematyczną:

\[ P(A|Q=q) = p_{Reszka|Q}(Reszka|Q = q) = q, \]

i z twierdzenia o pełnym prawdopodobienstwie możemy znaleźć \(P(A)\):

\[ P(A) = \int_0^1f(q)p_{Reszka|Q}(Reszka|Q = q) dq = \int_0^1 3q^2\cdot q dq = \frac{3}{4}. \]

Takie zadania zwykle są proste, gdy analityczne rozwiązanie mamy przed oczami. Jeżeli nie jesteśmy pewni swojego wyniku, to możemy po prostu sytuację zasymulować! Z R prawdopodobieństwo i statystyka stają się dziedzinami eksperymentalnymi.

Najpierw wolosujmy sobie 1000000 liczb z naszego rozkładu:

n <- 1000000
coinBiases <- myGenerator(n, invTransFunction)

i porzucajmy monetą

tossesA <- sapply(coinBiases, 
                  function(x) sample(c(1,0), 1, prob = c(x, 1-x)))
headProbability <- mean(tossesA)
headProbability

## [1] 0.750148

Każdy rzut jest wykonywany inną monetą - prawdopodobieństwo reszki dla każdej z nich jest wylosowane z rozkładu \(f(q)\). Wykonaliśmy 1000000 rzutów różnymi monetami i uzyskaliśmy proporcję reszek równą 0.750148 - wynik ten jest zgodny z naszymi wcześniejszymi obliczeniami. Nie jest to żaden dowód - jedynie numeryczne potwierdzenie prawidłowości wyniku.

Popatrzmy jeszcze przez chwilę na kawałek kodu powyżej: sapply(coinBiases, function(x) sample(c(1,0), 1, prob = c(x, 1-x))). Funkcja sapply każdy element wektora coinBiases (prawdopodobieństwa reszek) wysyla do anonimowej funkcji, która jednokrotnie “rzuca monetą”. W wyniku otrzymujemy wektor rzutów monetą - funkcja sapply stara się uprościć wynik (stąd sapply, s - jak simplify) i zwrócić go nam w jak najprostszej postaci.

condProb <- mean(coinBiases[tossesA == 1] > 0.69 & coinBiases[tossesA == 1] < 0.71)
condProb

## [1] 0.02743059

tossesB <- sapply(coinBiases, function(x) sample(c(1,0), 1, prob = c(x, 1-x)))

condProbB <- sum(tossesB == 1 & tossesA == 1)/sum(tossesA == 1)
condProbB

## [1] 0.7998488